Temperature control modes
While thermostats typically operate only in the on/off mode, the electronic controllers can regulate in two main modes: on/off with adjustable differential or PID.
1. ON/ OFF ACTION
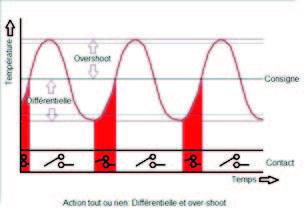
In the On/Off action, the heater is off when the set point is reached, and restarted when the temperature drops below the set point value minus the differential. This is the conventional mechanical thermostats operating mode. The successful operation of this mode mainly depends on the temperature sensor correct positioning near the heat source and the compatibility between the heating power and the need of the environment to be heated. The On/Off action does not usually prevent temperature peaks (over-shoot) after switching off the heating, due to the system thermal inertia.
2. ADJUSTABLE DIFFERENTIAL
A low differential is often associated with control accuracy. However, a too low differential will cause heating short cycles and premature contact wear if a power relay is used, or a quick degradation of the compressor if the system is used to control a refrigerator. The electronic controllers in this catalog have an adjustable differential to optimize this operation.
3. THE PID ACTION
(Acronym for proportional, integral and derivative).
The PID action is a control mode that involves the concept of Feedback. Simply speaking, this means that the regulator will analyze what temperature rise will be produced by a quantity of energy supplied to the heating device and how long this rise in temperature will take. This action involves three different settings:
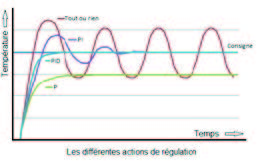
Proportional band: : this band is an area before the set point, in which the electronic controller will gradually decrease the power it provides to the heating device. At the furthest end from the set point, the power will be 100%, to reach 0% when the set point is reached. The purpose of the proportional band is to avoid the over-shoot phenomenon. This variation of power is obtained by gradually reducing the warm-up time as the temperature approaches the set point. The larger the band is, the longer it takes to reach the set point. A proportional action only is generally not sufficient to reach the set point as the temperature stabilization is made below the set point, due to heat losses and exchanges.
This lack of proportional action is corrected by the integral action. This integral action will continue to provide a heating control signal as long as the heating temperature of the heating device is not equal to the set point. In this purpose it also integrates the time for the system to heat up.
This action is equal to the integral of the deviation from the set point divided by a time constant. This time constant corresponding to the setting I. When the integral time is set to 0, a simple proportional action is obtained. The proportional-integral action allows the set point value to be reached after a few oscillations when starting the process.
We can limit these oscillations by introducing another correction: the derivative action, which allows to anticipate overshoots.
The derivative action adjusts the output power from the temperature variation curve. It involves predicting temperature variations based on previous actions of the output signal. By predicting temperature variations based on previous actions of the output signal, it compensates the response times due to the thermal inertia, accelerates the response of the system and enhances the stability of the loop, while allowing a quick damping of the oscillations due to the occurrence of a disturbance or a sudden variation of the set point.
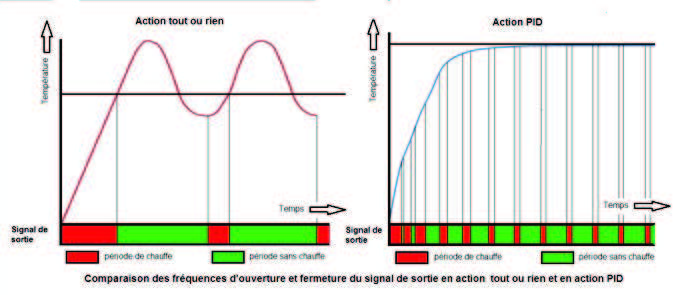
If the PID action can improve the control in a number of configurations, the drawback is that the output signal will cycle very quickly, which reduces the power relay life very extensively and requires in most cases to use solid state relays.
4. THE AUTO-TUNE FUNCTION (SELF ADJUSTABLE)
Determining the P, I, D, parameters, which is possible by calculation or by successive approximations, is a tedious and complex operation. The new generation of auto-tune regulators will analyze how the thermal system will react during two functioning On/0ff cycles, then automatically compute the optimum PID parameters.
